The formulas that follow extract how many parts there are in a layout drawing.
NOTE: If a formula is applied to a drawing that has no parts, the result is 0.
| Counting | In | The formula |
|---|---|---|
| All 1ups | LayoutN | LayoutN.PartsCount() |
| OneUpN | LayoutN | LayoutN.PartsCount(OneUpN) |
| OneUpN.PartsCount(LayoutN) | ||
| OneUpN | All layouts | OneUpN.PartsCount() |
TIP: When typing functions, you can cite the names of drawings instead of the names of the system names OneUpN or LayoutN. Note, however, that using this approach requires that you follow a strict naming convention for your 1ups and layouts.
Two 1ups are arrayed in two layouts. The 1ups are named Rectangle and Ellipse. The layout names are Layout A and Layout B.
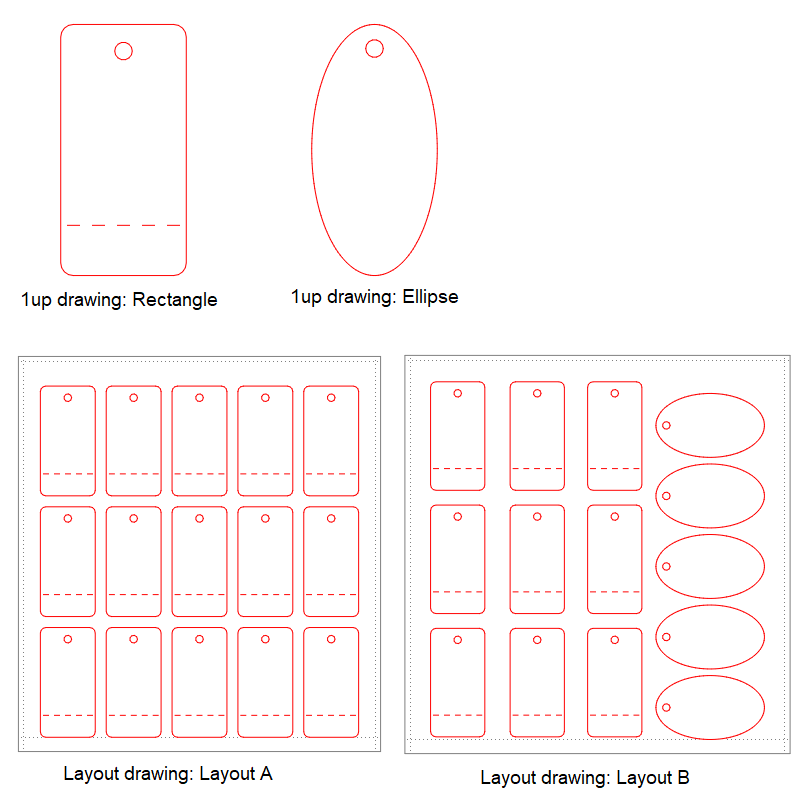
NOTE: Create a print drawing by using a design frame in which the formulas use system namenames:
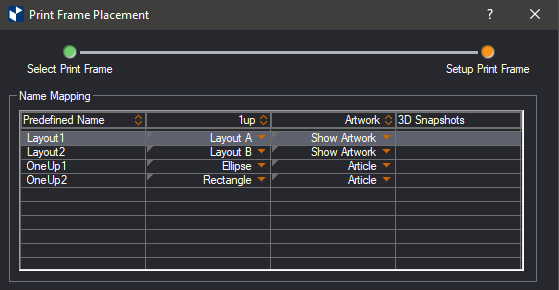
| To count | In | Use | Example |
|---|---|---|---|
| 1ups | Layout1 | $Layout1.PartsCount(); n0$ | 15 |
| 1ups | Layout2 | $Layout2.PartsCount(); n0$ | 14 |
| OneUp1 parts | Layout1 | $Layout1.PartsCount(OneUp1); n0$ | 0 |
| OneUp1 | $OneUp1.PartsCount(Layout1); n0$ | ||
| OneUp1 | Layout2 | $Layout2.PartsCount(OneUp1); n0$ | 5 |
| $OneUp1.PartsCount(Layout2); n0$ | |||
| OneUp1 parts | All layouts | $OneUp1.PartsCount(); n0$ | 5 |
| OneUp2 parts | $OneUp1.PartsCount(); n0$ | 24 |
NOTE: The n0 rounding identifier displays the result without a fractional part.
| With Semicolon | With Comma |
|---|---|
| $Layout1.Length(Cutting; m; yes); n2$ | $Layout1.Length(Cutting, m, yes), n2$ |
The following are examples in which formulas use specific drawing names:
| Drawing | Layout | Use | Example |
|---|---|---|---|
| All drawings | "Layout A" | $"Layout A".PartsCount(); n0$ | 15 |
| "Ellipse" | "Layout B" | $"Layout B".PartsCount(Ellipse); n0$ | 5 |
| $Ellipse.PartsCount(Layout B); n0$ | |||
| "Rectangle" | All layouts | $Rectangle.PartsCount(); n0$ | 24 |